In this post we will be learning about various types of beams used in engineering mechanics and their deflected shape on uniform loading.
There are basically 6 types of beams used in mechanics. Beams used for finding out reactions on support are assumed to be massless and the support, if pinned or roller, are frictionless. This is assumed to for the sake of easy calculations.
Simply Supported Beam
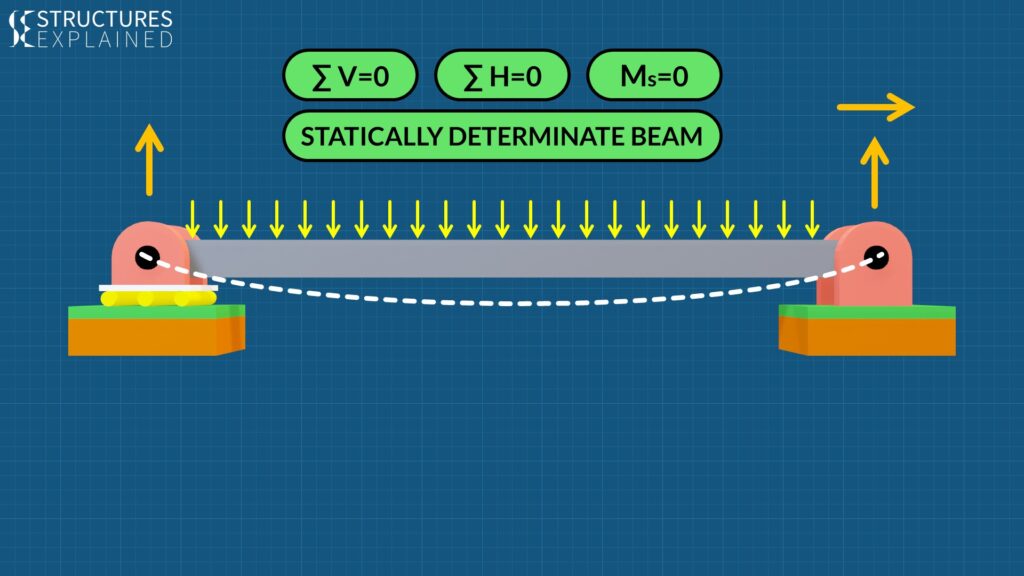
Starting from the simplest of the beams, the simply supported beam rests on a pin and roller support. Pin support allows rotation and roller support allow rotation and lateral movement. The deflected shape of the beam on loading is shown in white dashed line. This beam has got 3 unknown reactions which are vertical reactions at both the support and a horizontal reaction at pin support. We have 3 equilibrium equations which are summation of forces in vertical direction is zero, summation of forces in horizontal direction is zero and moment about any of the support as zero, to find the 3 reactions. Hence it is called a statically determinate beam.
Overhanging Beam
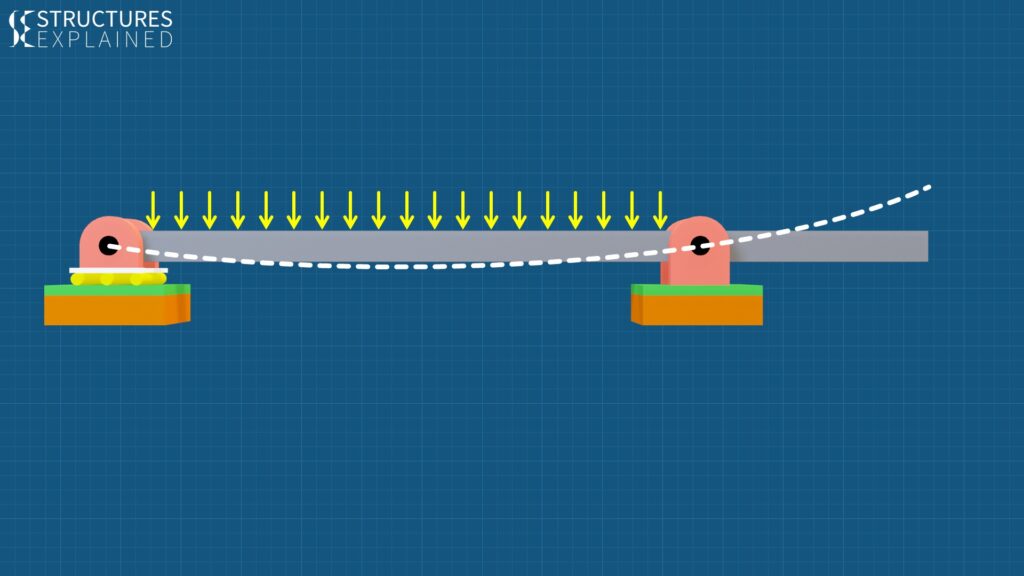
Next we are looking at an overhanging beam in which some portion of the beam extends from the support from one side. The deflected shape of the beam on uniform loading between supports would look line white dashed line, in which both the supports will allow rotation of the beam.
If the overhang is from both the ends, then the beam is supposed to be called, double overhang and the deflected shape on uniform loading would look something like this. These arrangements are also statically determined with 3 unknowns and 3 equilibrium equations.
Fixed Beam
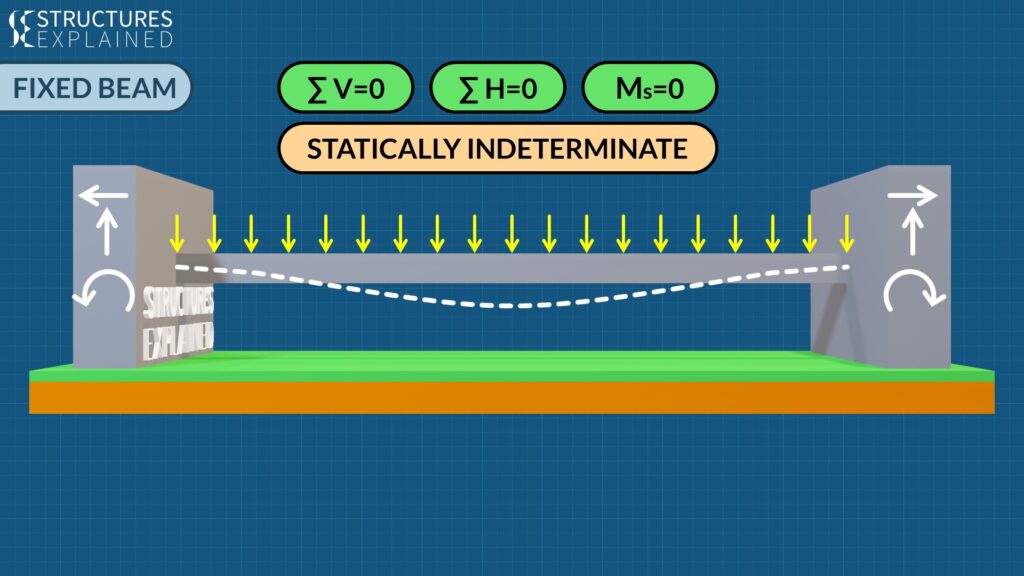
Next is, Fixed beam, which has fixed or rigid supports from both the ends. Deflected shape due to uniform loading will look something like white dashed line in which fixed supports will not rotate. Fixed support gives all 3 reactions which are horizontal, vertical and moment at both supports hence a total of 6 unknowns. These unknowns cannot be found by 3 equilibrium equations hence the arrangement is called statically indeterminate.
Cantilever Beam
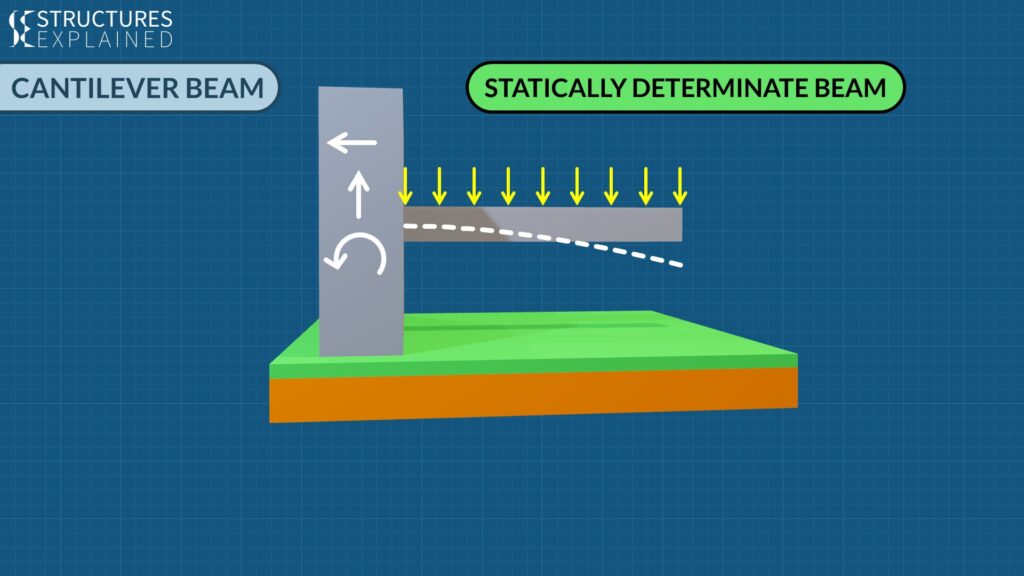
Next we will see a cantilever beam, which is fixed on one side and free on the other side. Deflected shape due to loading will look something like white dashed line. This beam has got only 3 unknowns hence they can be found by equilibrium equations making this beam statically determinate.
Propped Cantilever
Next we will see a propped cantilever beam which is nothing but a cantilever beam with a Roller support at the other end. The deflected shape due to loading on the propped cantilever will look something like white dashed line. As the total number of unknown reactions are 4, 3 from fixed support and one from roller, it will be termed as a statically indeterminate beam.
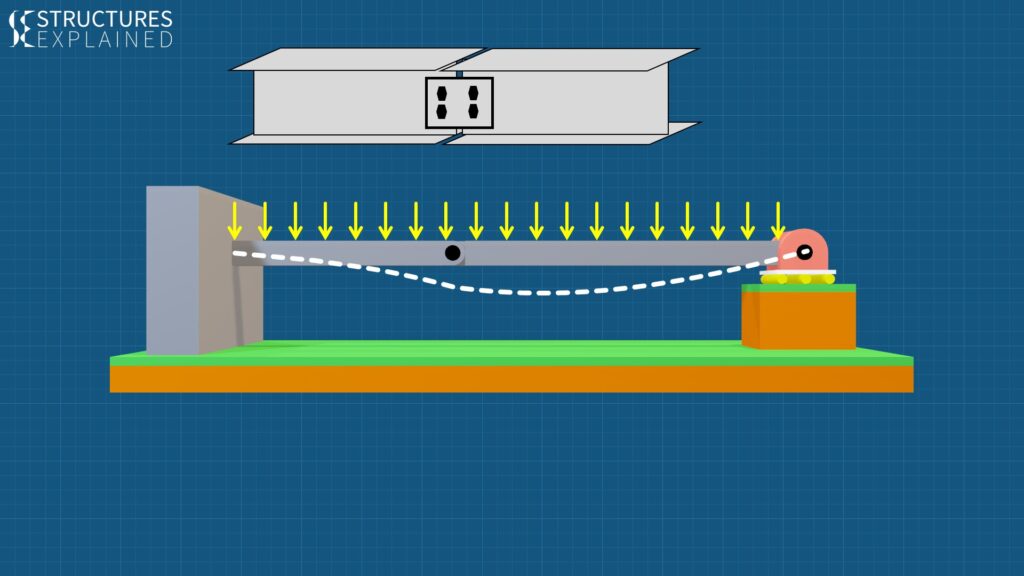
But what if I tell you that a propped cantilever can be made statically determinate? This can be possible by introducing an internal hinge or pin. Internal hinge allows free rotation hence moment at that point is zero. Beams to the left and right of the internal hinge can be treated like 2 separate beams for calculations. Deflections due to uniformly distributed load in this case would look something like white dashed line. The slope abruptly changes on each side of the hinge. In the real world a shear connection between 2 beams can be assumed as an internal hinge.
Continuous Beam
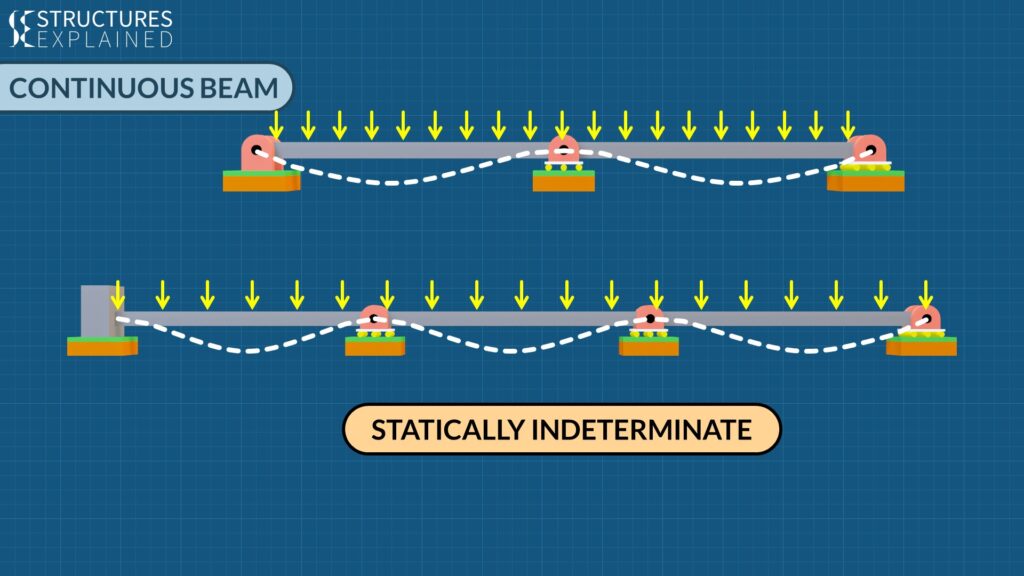
Next comes a continuous beam which has 2 or more than 2 spans. The support at the ends may be fixed, pinned or roller. The ends can be overhanging or supported. Deflected shape of the continuous beam on loading will look something like the white dashed line. Point to be noted here is that the intermediate support will not allow rotation of the beam hence there will be some amount of bending moment present at that support. As the unknown reactions in a continuous beam are more than 3, the reactions cannot be statically determined.
Also read ๐ Types of Support | Support Reactions in a Beam
Watch in video form.
I go to see day-to-day a few blogs and sites to read content, except
this web site offers quality based posts.
Hi! I could have sworn I’ve been to this blog before
but after reading through some of the post I realized it’s new to me.
Nonetheless, I’m definitely glad I found it and I’ll be bookmarking and checking back frequently!
Artigo fantรกstico .Muito Claro e de simples compreensรฃo .
top !
รฉ legal saber que que ainda tem pessoas que criam materiais que auxiliam outras pessoas.
muito sucesso para vocรช
I go to see everyday a few sites and websites to read articles or reviews,
but this web site presents feature based posts.
Olรก vocรช tem idรฉia de como gerar dinheiro somando o que vocรช
trata nesta pรกgina , com a psicologia ? Sei que a pergunta parece estranha , mas este รฉ um plano que tenho hรก tempos e depois de ler
seu blog a cabeรงa ficou a milhรฃo
eu gosto muito quando me deparo com materiais tรฃo bem escritos quanto o
que encontrei neste portal . Continuarei visitando seu site pois
adorei dos seus textos .
Tremendous things here. I’m very satisfied to look your post.
Thank you a lot and I am having a look ahead to touch you.
Will you kindly drop me a mail?
I’m amazed, I have to admit. Seldom do I encounter a blog that’s both educative and engaging, and without a doubt, you’ve hit the nail on the
head. The problem is something not enough folks are speaking intelligently about.
Now i’m very happy that I found this in my search for
something concerning this.
Hello There. I found your blog using msn. This is
an extremely well written article. I’ll be sure to bookmark it and return to read
more of your useful info. Thanks for the post.
I will certainly return.
This website certainly has all the info I needed about this subject and didn’t know who to
ask.
Olรก , tudo vai bem ? ร claro que vocรช estรก compartilhando fatos com propriedade , isso
รฉ excelente , continue escrevendo!
I visited multiple websites but the audio feature for audio songs current at this web site is genuinely
superb.
Saved as a favorite, I like your site!
Hi are using WordPress for your blog platform? I’m new to the
blog world but I’m trying to get started and set up my own. Do you require any coding expertise to make your own blog?
Any help would be really appreciated!
Hi to all, as I am genuinely eager of reading this weblog’s post to
be updated regularly. It includes pleasant information.
After exploring a number of the blog articles on your site,
I seriously like your technique of blogging. I book
marked it to my bookmark site list and will be checking back in the near future.
Please visit my web site as well and tell me
what you think.
When someone writes an article he/she keeps the
plan of a user in his/her mind that how a user can know it.
Thus that’s why this article is great. Thanks!
Simply want to say your article is as amazing.
The clearness on your post is just spectacular and i could assume you
are an expert on this subject. Fine along with your permission allow me to seize
your feed to keep up to date with coming near
near post. Thanks a million and please continue the rewarding work.
Hello, its fastidious post concerning media print, we all be familiar with
media is a fantastic source of facts.
Good respond in return of this matter with solid arguments and explaining the whole thing on the topic
of that.
Hello! I know this is kind of off topic but I was wondering if you knew where I could locate a captcha plugin for my comment form?
I’m using the same blog platform as yours and I’m having
trouble finding one? Thanks a lot!
sempre que tenho um minuto eu venho ler neste site .
os artigos sรฃo sempre muito bem elaborado e simples de
entender . Atรฉ breve
Right here is the right webpage for everyone who would like to understand this topic.
You know so much its almost hard to argue with you (not that I
really will need toโฆHaHa). You certainly put a brand new spin on a topic that has been discussed for many years.
Wonderful stuff, just excellent!
Excelente post! Jรก vi que terei que voltar
a esse website muitas vezes para saber mais sobre o assunto .
Hi, I read your blog on a regular basis. Your humoristic style is witty, keep doing what you’re doing!
For most recent information you have to pay a quick visit web and on internet I found this web page
as a most excellent web page for most up-to-date updates.
I want to to thank you for this great read!! I absolutely loved every bit of it.
I have you saved as a favorite to look at new stuff you postโฆ
Hello! This is my first comment here so I just wanted
to give a quick shout out and tell you I genuinely enjoy reading through your articles.
Can you recommend any other blogs/websites/forums
that cover the same subjects? Thanks a lot!
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point.
You clearly know what youre talking about, why waste
your intelligence on just posting videos to your blog when you could be giving
us something enlightening to read?
This paragraph will assist the internet viewers for setting up
new blog or even a blog from start to end.
excellent put up, very informative. I wonder why the other specialists of this sector don’t realize this.
You must proceed your writing. I am sure, you have
a great readers’ base already!
Your mode of explaining the whole thing in this paragraph is genuinely good, all be capable of
effortlessly understand it, Thanks a lot.
I like the valuable info you provide to your articles. I will bookmark
your blog and take a look at again right here frequently.
I am relatively certain I’ll learn many new stuff
right here! Good luck for the next!
Way cool! Some extremely valid points! I appreciate
you penning this article plus the rest of the website is very good.
I know this site offers quality dependent articles and additional stuff, is there any other web site which gives these kinds of data in quality?
Wow, amazing blog layout! How long have you been blogging for?
you make running a blog glance easy. The full look of your website is great,
let alone the content!
Iโm not that much of a internet reader to be honest but your blogs really
nice, keep it up! I’ll go ahead and bookmark your
site to come back down the road. Cheers
Hello There. I found your blog using msn. This
is an extremely well written article. I will be
sure to bookmark it and return to read more of your useful information. Thanks for the post.
I will certainly comeback.
I needed to thank you for this excellent
read!! I definitely loved every bit of it.
I’ve got you book-marked to look at new things you postโฆ
I think this is among the most significant info for me.
And i am glad reading your article. But should remark on few general things, The web site style is great,
the articles is really great : D. Good job, cheers
Olรก , gosto de ler todos dos artigos do seu site. Estou passando
apenas para parabenizar vocรช. Abraรงos
Write more, thats all I have to say. Literally,
it seems as though you relied on the video to make your point.
You definitely know what youre talking about, why throw away your intelligence on just posting videos to your weblog when you could be giving us something enlightening to read?
I simply couldn’t leave your web site prior to suggesting that I extremely
loved the standard info an individual provide to your visitors?
Is gonna be back ceaselessly in order to check up on new posts
Superb, what a weblog it is! This webpage gives valuable facts to us,
keep it up.
I’ve been exploring for a little for any high quality articles or weblog posts in this kind of house .
Exploring in Yahoo I at last stumbled upon this web site.
Reading this info So i am satisfied to express that I’ve a very excellent uncanny feeling I came upon just what I needed.
I such a lot indubitably will make certain to do not put out of your mind
this site and provides it a glance regularly.
Wonderful items from you, man. I have take into account your stuff previous to and you’re simply too wonderful.
I actually like what you’ve received here, certainly like what you are saying and the best way in which you assert it.
You are making it enjoyable and you still take care of to keep it sensible.
I can’t wait to read far more from you. This is really a tremendous web site.
What a material of un-ambiguity and preserveness of
valuable knowledge concerning unpredicted feelings.
I don’t even know how I ended up here, but I thought this post was good.
I do not know who you are but certainly you are going to a famous blogger if you aren’t already ๐ Cheers!
We’re a group of volunteers and opening a new scheme in our community.
Your website offered us with valuable info to work on. You’ve done a formidable job and our entire
community will be thankful to you.
I really like what you guys are up too. This type of clever work and reporting!
Keep up the great works guys I’ve added you guys to blogroll.
Hi there, You’ve done an incredible job. I will definitely digg it and personally recommend to my friends.
I am sure they will be benefited from this site.
Hi everyone, it’s my first visit at this website, and piece of writing is truly fruitful designed
for me, keep up posting these articles or reviews.
Hey there are using WordPress for your blog platform?
I’m new to the blog world but I’m trying to get started and create my own. Do you require
any html coding knowledge to make your own blog? Any
help would be greatly appreciated!
Hello my family member! I want to say that this
article is awesome, great written and include approximately all vital infos.
I would like to see extra posts like this .
Greate article. Keep writing such kind of info on your page.
Im really impressed by it.
Hello there, You have done a fantastic job. I will certainly digg it and personally suggest
to my friends. I’m confident they will be benefited from this
site.
Good day! This post could not be written any better! Reading through this post reminds me of my good old room mate!
He always kept chatting about this. I will forward this page to him.
Pretty sure he will have a good read. Many thanks for
sharing!
Hello every one, here every one is sharing such familiarity, so
it’s good to read this webpage, and I used to go to see this webpage every day.
Good site you have got here.. It’s difficult to find excellent writing like yours these days.
I really appreciate people like you! Take care!!
I enjoy reading through an article that can make people think.
Also, thank you for allowing for me to comment!
Hi there, yup this paragraph is really pleasant and I have learned lot
of things from it concerning blogging. thanks.
Hello There. I discovered your blog the usage of msn. This
is an extremely well written article. I will make sure to bookmark it
and come back to learn extra of your useful info. Thanks for the post.
I’ll definitely return.
Hello! Someone in my Myspace group shared this website with us so I
came to check it out. I’m definitely loving the information. I’m
bookmarking and will be tweeting this to my followers!
Fantastic blog and superb design.
naturally like your website however you need to check the spelling on quite a few of your posts.
Several of them are rife with spelling problems and I to find it very bothersome to inform the truth
nevertheless I’ll certainly come back again.
Everything is very open with a precise description of the issues.
It was truly informative. Your site is extremely helpful.
Many thanks for sharing!
Touche. Sound arguments. Keep up the great spirit.
Saved as a favorite, I love your website!
Hello! This is my first comment here so I just wanted to give a quick shout out
and tell you I really enjoy reading through your blog posts.
Can you recommend any other blogs/websites/forums that go over the same
topics? Thanks!
I have been surfing online more than 3 hours today, yet I never found any interesting article like yours.
It is pretty worth enough for me. In my opinion, if all web owners and bloggers made good content as you did, the internet will
be much more useful than ever before.
Hello, i think that i saw you visited my weblog so i came to โreturn the favorโ.I am attempting to
find things to improve my web site!I suppose its ok to use a few
of your ideas!!
Thank you, I’ve recently been looking for info about this subject for a long
time and yours is the greatest I’ve came upon till
now. However, what in regards to the bottom line?
Are you positive in regards to the source?
I all the time used to read paragraph in news papers
but now as I am a user of web so from now I am using net for articles, thanks to web.
Hiya very cool site!! Guy .. Beautiful .. Superb ..
I’ll bookmark your web site and take the feeds also?
I’m happy to seek out a lot of useful information right here within the post, we want
develop extra techniques on this regard, thank you for sharing.
. . . . .
Hi there I am so glad I found your website, I really
found you by mistake, while I was searching on Yahoo for something else, Nonetheless I am here now and would just
like to say thanks a lot for a fantastic post and a all round interesting blog (I also love the theme/design), I don’t have time to go through it all at the
minute but I have saved it and also added in your RSS feeds,
so when I have time I will be back to read much more, Please
do keep up the superb work.
Remarkable issues here. I’m very glad to peer your article.
Thanks a lot and I’m having a look ahead to touch you. Will you kindly drop me
a e-mail?
This site was… how do you say it? Relevant!! Finally I’ve found something that helped me.
Cheers!
We are a group of volunteers and opening a new scheme in our community.
Your site offered us with valuable info to work on. You’ve done an impressive job and our entire community
will be thankful to you.
Excellent blog you have here.. It’s difficult to find excellent writing like yours these days.
I seriously appreciate individuals like you! Take care!!
Hello, all is going fine here and ofcourse every one
is sharing facts, that’s in fact good, keep up writing.
whoah this blog is wonderful i really like studying your
posts. Keep up the good work! You know, many individuals
are hunting around for this info, you could aid them
greatly.
Whats up very nice website!! Man .. Beautiful .. Wonderful ..
I will bookmark your site and take the feeds
additionally? I am glad to search out a lot of helpful information right
here in the submit, we’d like work out extra strategies on this regard, thanks for sharing.
. . . . .
When someone writes an post he/she keeps the image of a
user in his/her brain that how a user can understand it.
Therefore that’s why this post is great. Thanks!
I’m very pleased to uncover this web site. I need to to thank you for your time due to this fantastic read!!
I definitely liked every little bit of it and I have you bookmarked
to check out new things in your web site.
We absolutely love your blog and find the majority of your post’s to be
exactly I’m looking for. Do you offer guest writers to write content for you
personally? I wouldn’t mind creating a post or elaborating on a
few of the subjects you write related to here. Again, awesome website!
Hello there! This article could not be written much better!
Looking at this post reminds me of my previous roommate!
He always kept talking about this. I most certainly will send this post to him.
Fairly certain he will have a good read. Thank you for sharing!
Attractive section of content. I just stumbled
upon your site and in accession capital to assert that I acquire in fact
enjoyed account your blog posts. Any way I
will be subscribing to your augment and even I achievement you access consistently fast.
With havin so much content and articles do you ever run into any problems of plagorism or copyright violation? My
blog has a lot of completely unique content I’ve either created myself or outsourced but it seems a lot of it is popping
it up all over the internet without my permission. Do you know any methods to help reduce content from being
ripped off? I’d genuinely appreciate it.
WOW just what I was searching for. Came here by searching for
website
Hi there this is kinda of off topic but I was wanting to know if blogs use WYSIWYG editors or
if you have to manually code with HTML. I’m starting a blog soon but have no coding expertise so I wanted to get advice from someone with experience.
Any help would be greatly appreciated!
Attractive section of content. I just stumbled upon your site and in accession capital
to assert that I acquire in fact enjoyed account your blog posts.
Anyway I will be subscribing on your augment or even I fulfillment you get
entry to constantly fast.
Hi there, yup this article is in fact fastidious and I have learned lot of
things from it on the topic of blogging. thanks.
Nice blog! Is your theme custom made or did you download it from somewhere?
A theme like yours with a few simple adjustements
would really make my blog jump out. Please let me know where you
got your theme. Thanks
I know this if off topic but I’m looking into starting my own blog and was
curious what all is required to get set up?
I’m assuming having a blog like yours would cost a pretty penny?
I’m not very internet savvy so I’m not 100% sure.
Any tips or advice would be greatly appreciated.
Cheers
Hi! I know this is somewhat off topic but I was wondering if you knew where I could get
a captcha plugin for my comment form? I’m using the same blog platform as yours and I’m having trouble finding one?
Thanks a lot!
If you want to get a great deal from this piece of writing then you have to apply these techniques to your won blog.
Hmm it appears like your website ate my first comment (it was extremely long) so
I guess I’ll just sum it up what I submitted and say, I’m thoroughly enjoying your blog.
I too am an aspiring blog blogger but I’m still new
to the whole thing. Do you have any suggestions for
rookie blog writers? I’d definitely appreciate it.
Hey there! I know this is kind of off topic but I was wondering if you knew where I could get a captcha plugin for my comment form?
I’m using the same blog platform as yours and I’m having difficulty finding one?
Thanks a lot!
hello!,I really like your writing so much! share we keep up a correspondence extra approximately your article on AOL?
I require a specialist in this house to unravel my
problem. Maybe that’s you! Taking a look ahead to peer you.
Very good post! We will be linking to this great content on our site.
Keep up the good writing.
I’d like to find out more? I’d like to find out some additional information.
When I initially left a comment I appear to have clicked on the -Notify me when new comments are
added- checkbox and from now on each time a comment is added I
receive four emails with the exact same comment.
Is there a means you can remove me from that service? Many thanks!
Hey there would you mind stating which blog platform you’re working
with? I’m looking to start my own blog in the near future but I’m having a hard time choosing between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your layout seems different then most blogs and I’m looking for something completely unique.
P.S Sorry for being off-topic but I had to ask!
WOW just what I was looking for. Came here by searching for website
Hello i am kavin, its my first occasion to commenting anyplace, when i read this piece of writing i
thought i could also create comment due to this good
piece of writing.
Thanks for the marvelous posting! I quite enjoyed reading it,
you’re a great author. I will always bookmark your blog and will come back very soon.
I want to encourage yourself to continue your great writing, have
a nice day!
Howdy! Would you mind if I share your blog with my zynga group?
There’s a lot of folks that I think would really appreciate
your content. Please let me know. Cheers
Hi there colleagues, how is all, and what you
desire to say regarding this article, in my view its
truly awesome designed for me.
Unquestionably believe that which you stated. Your favorite reason appeared to be on the internet the simplest
thing to be aware of. I say to you, I definitely get irked while people consider worries that they just don’t know about.
You managed to hit the nail upon the top as well as defined out the whole thing without having side-effects , people could take a signal.
Will likely be back to get more. Thanks
I like it when people come together and share opinions.
Great site, keep it up!
Hi there, You’ve done an incredible job. I’ll definitely
digg it and personally recommend to my friends. I’m sure they will be benefited from this web site.
This piece of writing is in fact a fastidious one it
helps new web users, who are wishing in favor of blogging.
Greate article. Keep writing such kind of info on your page.
Im really impressed by your site.
Hi there, You’ve performed a great job. I will certainly digg it and in my view recommend to my
friends. I’m confident they’ll be benefited from this web
site.
I love looking through a post that can make people
think. Also, thanks for allowing for me to comment!
Thanks very nice blog!
Howdy I am so happy I found your blog, I really found you by accident, while I was
searching on Google for something else, Nonetheless I am here now and would just like to say cheers
for a tremendous post and a all round interesting blog
(I also love the theme/design), I don’t have time to look over it all at the minute but I
have saved it and also included your RSS feeds, so when I have time I will be back to read a great deal more, Please do keep up the excellent work.
This design is spectacular! You certainly know how to keep a reader entertained.
Between your wit and your videos, I was almost moved to start
my own blog (well, almost…HaHa!) Excellent job. I really loved what you had to say, and
more than that, how you presented it. Too cool!
Thankfulness to my father who stated to me concerning this website,
this web site is actually awesome.
Do you mind if I quote a few of your posts as long as I
provide credit and sources back to your blog?
My blog site is in the very same niche as yours and my visitors would really benefit from some
of the information you present here. Please let
me know if this okay with you. Thanks!
Spot on with this write-up, I really feel this website needs a great deal
more attention. I’ll probably be returning to read more, thanks for the
advice!
Having read this I thought it was extremely informative.
I appreciate you finding the time and energy to
put this informative article together. I once again find myself spending way too much time both reading and posting comments.
But so what, it was still worth it!
Hello, i read your blog occasionally and i own a similar one and i was just wondering if you get a lot of spam responses?
If so how do you stop it, any plugin or anything you can suggest?
I get so much lately it’s driving me mad so any assistance is very much appreciated.
Pretty nice post. I just stumbled upon your blog and wished to say that I’ve truly enjoyed browsing
your blog posts. In any case I will be subscribing
to your rss feed and I hope you write again soon!
Write more, thats all I have to say. Literally, it seems as though you relied on the video to make your point.
You obviously know what youre talking about, why throw
away your intelligence on just posting videos to your blog when you could be
giving us something enlightening to read?
Hi all, here every person is sharing these know-how, so it’s fastidious
to read this weblog, and I used to visit this web
site all the time.
Helpful information. Fortunate me I discovered your site accidentally,
and I’m stunned why this accident didn’t took place earlier!
I bookmarked it.
I’m amazed, I have to admit. Rarely do I come across a blog that’s
both equally educative and amusing, and without a doubt, you’ve hit the nail on the head.
The issue is an issue that not enough men and women are
speaking intelligently about. I am very happy I found this during my search for something relating
to this.
You really make it seem so easy with your presentation but I
find this topic to be really something which I think I would never understand.
It seems too complex and very broad for me. I’m looking forward for your next post, I will try to
get the hang of it!
Hello there! This is kind of off topic but I need some guidance from an established blog.
Is it difficult to set up your own blog? I’m not very techincal but I can figure
things out pretty fast. I’m thinking about making my own but I’m not sure where to begin. Do you have any tips or suggestions?
Many thanks
I’ve been surfing online more than 3 hours today, yet I never found
any interesting article like yours. It is pretty worth enough for me.
Personally, if all webmasters and bloggers made good content as you
did, the internet will be a lot more useful than ever before.
obviously like your web site but you have to test the spelling
on quite a few of your posts. A number of them are rife with spelling issues
and I to find it very bothersome to inform the reality then again I will certainly come back
again.
Hey there! This is my 1st comment here so I just wanted to
give a quick shout out and say I genuinely enjoy reading
through your posts. Can you suggest any other blogs/websites/forums that go over the same topics?
Thank you!
Hey! Quick question that’s totally off topic.
Do you know how to make your site mobile friendly?
My website looks weird when browsing from my iphone4.
I’m trying to find a theme or plugin that might be able to
fix this problem. If you have any suggestions, please share.
Thanks!
Hey! I know this is kinda off topic however , I’d figured I’d ask.
Would you be interested in exchanging links or maybe guest authoring
a blog article or vice-versa? My website covers a lot of the same
subjects as yours and I feel we could greatly benefit from each other.
If you are interested feel free to send me an email. I look
forward to hearing from you! Terrific blog by the way!
I’m really enjoying the theme/design of your website.
Do you ever run into any web browser compatibility issues?
A few of my blog readers have complained about my
website not working correctly in Explorer but looks great in Firefox.
Do you have any recommendations to help fix this problem?
For the reason that the admin of this web site is working, no question very rapidly it
will be famous, due to its feature contents.
When some one searches for his required thing, thus he/she wants to be available that in detail, so that
thing is maintained over here.
I was recommended this blog by my cousin. I am not sure whether this post is written by him as no one else know such detailed
about my difficulty. You are incredible! Thanks!
These are truly great ideas in on the topic of blogging. You have touched some pleasant things here.
Any way keep up wrinting.
It’s remarkable to visit this web site and reading
the views of all friends about this paragraph, while I am also keen of getting
know-how.
Pretty nice post. I just stumbled upon your blog and wished to say that I have really enjoyed surfing around your blog
posts. In any case I will be subscribing to your feed and I hope you
write again very soon!
Fastidious response in return of this matter with
real arguments and describing everything on the topic of that.
This is my first time go to see at here and i am actually pleassant to read everthing at
one place.
Hey there! I’ve been following your weblog for some time now and finally got the courage to go ahead and give you
a shout out from Porter Tx! Just wanted to tell you keep
up the excellent work!
I have to thank you for the efforts you’ve put in penning this site.
I am hoping to see the same high-grade content from you in the future as well.
In fact, your creative writing abilities has encouraged me to get my very own website now ๐
It’s awesome to go to see this site and reading the views of all colleagues about this piece of writing, while I am also zealous
of getting know-how.
Good day! Do you use Twitter? I’d like to follow you if that would be okay.
I’m definitely enjoying your blog and look forward to new posts.
Thanks very interesting blog!
Hi there Dear, are you in fact visiting this website regularly, if so
then you will without doubt get pleasant experience.
wonderful issues altogether, you just received a emblem new reader.
What may you recommend in regards to your put up that you just made a few days ago?
Any sure?
Hi there, this weekend is good in favor of me, for the
reason that this time i am reading this great informative piece of writing here at my home.
Write more, thats all I have to say. Literally, it seems as though you relied on the video
to make your point. You obviously know what youre talking about,
why throw away your intelligence on just posting videos to your blog
when you could be giving us something enlightening to read?
Truly when someone doesn’t understand then its up to other people that they will help, so here it occurs.
Hi! I’m at work browsing your blog from my new iphone 3gs!
Just wanted to say I love reading your blog and look forward to all
your posts! Carry on the excellent work!
Incredible! This blog looks exactly like my old one! It’s on a completely different topic but it has pretty
much the same page layout and design. Excellent
choice of colors!
I think this is one of the most vital information for me.
And i’m glad reading your article. But should remark on some general things,
The website style is perfect, the articles
is really nice : D. Good job, cheers
Pretty element of content. I simply stumbled upon your weblog and in accession capital to say that I acquire actually enjoyed
account your weblog posts. Any way I will be subscribing in your feeds and even I
fulfillment you get entry to constantly quickly.
Hi Dear, are you actually visiting this web page daily, if so after that you will absolutely take pleasant knowledge.
Hey there! This is kind of off topic but I need some advice from
an established blog. Is it very difficult to set up your own blog?
I’m not very techincal but I can figure things out pretty fast.
I’m thinking about making my own but I’m not sure where to start.
Do you have any tips or suggestions? With thanks
In fact when someone doesn’t understand after that its up to other viewers that they will help, so here it takes place.
Hi, i read your blog from time to time and i own a similar one and i was just curious
if you get a lot of spam responses? If so how do you protect
against it, any plugin or anything you can recommend? I get so much
lately it’s driving me crazy so any assistance is very much appreciated.
Hi there i am kavin, its my first occasion to commenting anyplace, when i read this paragraph i
thought i could also make comment due to this good paragraph.
I visited various websites but the audio feature for audio songs current at this
web page is in fact wonderful.
Hello! This post couldn’t be written any better! Reading through this post reminds me of my good old room mate!
He always kept talking about this. I will forward this page to him.
Fairly certain he will have a good read. Thank you for sharing!
Hey there! This is kind of off topic but I need some advice from an established blog.
Is it very hard to set up your own blog? I’m not very
techincal but I can figure things out pretty fast. I’m thinking
about creating my own but I’m not sure where to start.
Do you have any ideas or suggestions? Many thanks
Hello, i think that i noticed you visited my blog so i came to go back the
favor?.I am attempting to to find things to improve
my website!I guess its ok to make use of some of your ideas!!
Post writing is also a excitement, if you be familiar with then you can write otherwise it is complex to write.
I know this if off topic but I’m looking into starting my own blog
and was wondering what all is required to get set up?
I’m assuming having a blog like yours would cost a pretty penny?
I’m not very web smart so I’m not 100% certain. Any tips
or advice would be greatly appreciated. Kudos
you’re in reality a good webmaster. The site loading velocity is
amazing. It kind of feels that you are doing any unique trick.
Moreover, The contents are masterpiece. you have done a fantastic process on this topic!
Hello mates, its fantastic piece of writing concerning tutoringand completely
defined, keep it up all the time.
Touche. Great arguments. Keep up the great work.
ะะณัะพะฒะพะน ัะพัั ะบะฐะถะดัะน ะผะตััั ะฟัะพะฒะตััะตััั ะฝะตะทะฐะฒะธัะธะผะพะน ะบะพะผะฟะฐะฝะธะตะน ะฝะฐ ัะพะพัะฒะตัััะฒะธะต ะทะฐะดะฐะฝะฝัะผ ะฟะฐัะฐะผะตััะฐะผ.
I pay a visit day-to-day a few websites and websites to read posts, except this website presents quality based content.
Quality articles or reviews is the main to interest the visitors to go to see the
web site, that’s what this web site is providing.
I read this paragraph fully about the comparison of most recent and earlier technologies, it’s awesome article.
I would like to thank you for the efforts you’ve put in writing this website.
I’m hoping to view the same high-grade blog posts by you in the future as well.
In fact, your creative writing abilities has inspired
me to get my own, personal blog now ๐
Normally I don’t read post on blogs, but I would like to
say that this write-up very forced me to try
and do it! Your writing taste has been surprised me.
Thanks, quite nice post.
Generally I do not learn post on blogs, however I would like to say that this write-up very compelled
me to check out and do it! Your writing taste has been amazed me.
Thank you, quite great article.
Hello, There’s no doubt that your site could be having web browser compatibility
issues. When I look at your web site in Safari, it looks fine but when opening in I.E., it’s got some overlapping issues.
I merely wanted to provide you with a quick heads up!
Apart from that, great site!
What’s Taking place i am new to this, I stumbled upon this I have found It positively helpful and it has helped me out loads.
I hope to contribute & aid different customers like its helped
me. Good job.
Hi, i think that i saw you visited my site thus i came to โreturn the favorโ.I am attempting to find things
to improve my site!I suppose its ok to use some of your ideas!!
Hello my friend! I wish to say that this article is awesome, great
written and come with almost all vital infos. I
would like to look extra posts like this .
Thank you for some other informative web site.
Where else may I get that kind of info written in such an ideal way?
I have a challenge that I’m just now working on, and I have been at
the glance out for such info.
Hello there! This post could not be written any better!
Reading through this post reminds me of my good old room mate!
He always kept chatting about this. I will forward this page to him.
Fairly certain he will have a good read. Thanks for sharing!
I have been exploring for a little for any high-quality articles or blog posts in this kind of
area . Exploring in Yahoo I at last stumbled upon this web site.
Reading this info So i’m glad to express that I have a very
good uncanny feeling I found out just what I needed.
I most surely will make sure to don?t overlook this site and provides it
a glance on a relentless basis.
I constantly spent my half an hour to read this weblog’s content
daily along with a cup of coffee.
Simply desire to say your article is as amazing. The clearness
in your post is simply cool and i can assume you are an expert
on this subject. Well with your permission allow me to grab your RSS feed to
keep updated with forthcoming post. Thanks a million and please keep up the rewarding work.
Nice blog! Is your theme custom made or did you download
it from somewhere? A theme like yours with a few simple tweeks would really make
my blog stand out. Please let me know where you got your
theme. Thank you
I simply couldn’t depart your web site before suggesting that I actually enjoyed the
standard information a person supply in your guests?
Is going to be again steadily in order to check out new posts
Its like you read my mind! You appear to know a lot about this,
like you wrote the book in it or something. I think that you can do with a few pics to drive the message
home a bit, but other than that, this is wonderful blog.
An excellent read. I’ll definitely be back.
Great blog you have got here.. It’s difficult to find excellent writing like yours
these days. I honestly appreciate people like you! Take care!!
Magnificent web site. Lots of useful info here.
I am sending it to a few buddies ans additionally sharing in delicious.
And certainly, thank you to your sweat!
Hi there! This is my first visit to your blog! We are a team of volunteers and
starting a new project in a community in the same niche.
Your blog provided us useful information to work on. You have done a extraordinary job!
Have you ever thought about creating an ebook or guest authoring on other websites?
I have a blog centered on the same information you discuss and would really
like to have you share some stories/information. I know my audience would enjoy your work.
If you are even remotely interested, feel free
to shoot me an e-mail.
Hello there, I found your site by the use of Google at
the same time as looking for a related topic, your web site got here up, it appears to be like great.
I have bookmarked it in my google bookmarks.
Hi there, simply become aware of your blog thru Google, and
found that it’s truly informative. I’m gonna be careful for brussels.
I will appreciate in the event you continue this in future.
A lot of other people will likely be benefited out
of your writing. Cheers!
I’m not sure where you are getting your information, but good topic.
I needs to spend some time learning more or understanding more.
Thanks for magnificent info I was looking for this info for my mission.
It’s really a great and helpful piece of info. I’m happy that you shared this helpful info with us.
Please keep us informed like this. Thank you for sharing.
Hey! This is my first comment here so I just wanted to give a
quick shout out and tell you I really enjoy reading through your posts.
Can you suggest any other blogs/websites/forums that deal
with the same subjects? Thanks!
I blog quite often and I really thank you for your content.
This article has truly peaked my interest. I’m going to bookmark your website and keep
checking for new information about once a week. I subscribed to your RSS
feed too.
Howdy! Would you mind if I share your blog with my zynga group?
There’s a lot of folks that I think would
really enjoy your content. Please let me know. Thank you
Hello There. I found your blog using msn. This is an extremely
well written article. I’ll make sure to bookmark it and come back to read
more of your useful info. Thanks for the post.
I’ll certainly return.
Hey! Quick question that’s totally off topic. Do you know how to make your site mobile friendly?
My site looks weird when viewing from my iphone. I’m
trying to find a theme or plugin that might be able to fix
this problem. If you have any recommendations, please share.
Thank you!
If some one wishes to be updated with most recent technologies
afterward he must be visit this web page and be up to date every day.
hello!,I love your writing so so much! proportion we keep in touch more approximately your article on AOL?
I need an expert in this space to resolve my problem.
May be that’s you! Looking forward to see you.
Hey! This is my first visit to your blog! We are a
team of volunteers and starting a new project in a community in the same niche.
Your blog provided us valuable information to work on. You have done a wonderful job!
Your means of telling the whole thing in this post is actually good, every one be capable of easily understand it, Thanks a lot.
I like the valuable info you provide on your articles.
I’ll bookmark your blog and take a look at again right here regularly.
I’m reasonably sure I’ll be informed many new stuff proper here!
Best of luck for the next!
What’s up to all, how is everything, I think every one is getting more from this web site, and your views are nice designed for new
viewers.
With havin so much content do you ever run into any issues of plagorism
or copyright infringement? My website has a lot of unique content I’ve
either authored myself or outsourced but it seems a lot of it is popping it up
all over the internet without my agreement. Do you know any methods to help protect against content from
being ripped off? I’d really appreciate it.
It’s hard to come by experienced people about this topic,
however, you sound like you know what you’re talking about!
Thanks
Hi! I’m at work browsing your blog from my new iphone 3gs!
Just wanted to say I love reading your blog and look forward to
all your posts! Carry on the fantastic work!
I used to be suggested this blog by means of my cousin. I am not certain whether this submit is written by means of him as
no one else realize such certain about my difficulty. You are incredible!
Thanks!
great points altogether, you just won a new
reader. What might you recommend in regards to your publish that you simply made a
few days in the past? Any certain?
Hey, I think your blog might be having browser compatibility issues.
When I look at your blog in Chrome, it looks
fine but when opening in Internet Explorer, it has some overlapping.
I just wanted to give you a quick heads up! Other then that,
very good blog!
Quality articles is the key to interest the users to go to see the website, that’s what this web page is providing.
This design is spectacular! You most certainly know how to keep a reader entertained.
Between your wit and your videos, I was almost moved to start my own blog (well, almost…HaHa!) Wonderful job.
I really enjoyed what you had to say, and more than that, how you presented it.
Too cool!
Simply desire to say your article is as astounding.
The clarity in your post is simply great and i could assume you’re an expert on this subject.
Well with your permission let me to grab your feed to keep updated with
forthcoming post. Thanks a million and please continue the
gratifying work.
Attractive section of content. I just stumbled upon your
web site and in accession capital to assert that I get in fact enjoyed account your blog posts.
Any way I will be subscribing to your feeds and even I achievement you access consistently
fast.
Magnificent site. Plenty of useful information here. I’m sending it to a few pals
ans additionally sharing in delicious. And obviously, thank you on your sweat!
Having read this I thought it was rather enlightening.
I appreciate you spending some time and effort to put this informative article together.
I once again find myself personally spending way too much time both reading and posting
comments. But so what, it was still worth it!
I all the time used to read paragraph in news papers but now
as I am a user of internet therefore from now I am using net for content, thanks
to web.
Unquestionably believe that which you said. Your favorite justification seemed to be on the
web the easiest thing to be aware of. I say to you, I definitely get irked while people consider worries that they plainly do
not know about. You managed to hit the nail upon the top and also defined out the whole
thing without having side-effects , people could take a signal.
Will probably be back to get more. Thanks
Woah! I’m really loving the template/theme of this website.
It’s simple, yet effective. A lot of times it’s challenging to get that “perfect balance” between user friendliness and
appearance. I must say that you’ve done a superb job with this.
In addition, the blog loads very quick for me on Safari.
Superb Blog!
Greetings from California! I’m bored to tears at work
so I decided to browse your website on my iphone during
lunch break. I really like the knowledge you provide here and can’t wait to take a look when I get home.
I’m amazed at how quick your blog loaded on my cell phone ..
I’m not even using WIFI, just 3G .. Anyways, wonderful blog!
Hey there would you mind stating which blog platform you’re
using? I’m going to start my own blog soon but I’m having a hard time selecting between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your design seems different then most
blogs and I’m looking for something unique.
P.S My apologies for getting off-topic but I had to ask!
I read this article fully about the resemblance of hottest and earlier technologies, it’s awesome
article.
Greetings from California! I’m bored at work so I decided to check out your
site on my iphone during lunch break. I love the information you provide here and can’t
wait to take a look when I get home. I’m shocked at how fast your
blog loaded on my cell phone .. I’m not even using WIFI, just 3G
.. Anyways, awesome site!
Thanks in support of sharing such a pleasant thinking, piece of writing is nice, thats why i have read it
completely
Hi there would you mind sharing which blog platform you’re
working with? I’m going to start my own blog soon but I’m
having a tough time choosing between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your layout seems different then most blogs and
I’m looking for something unique.
P.S My apologies for getting off-topic but I had to ask!
This is very interesting, You are a very skilled blogger.
I’ve joined your feed and look forward to seeking more of your wonderful
post. Also, I have shared your website in my social networks!
Have you ever thought about including a little bit more than just your articles?
I mean, what you say is important and everything.
But just imagine if you added some great visuals or
video clips to give your posts more, “pop”! Your content is
excellent but with pics and clips, this site could certainly be one of the most beneficial in its field.
Fantastic blog!
Have you ever considered about including a little bit more
than just your articles? I mean, what you say is important and everything.
However just imagine if you added some great graphics or videos to give your posts
more, “pop”! Your content is excellent but with pics and video clips,
this site could definitely be one of the greatest in its niche.
Good blog!
This information is priceless. How can I find out more?
Hi, I read your blog regularly. Your humoristic style is awesome, keep up the good work!
Wow! Finally I got a blog from where I be capable of really take useful facts regarding my
study and knowledge.
If you desire to improve your know-how just keep visiting this
site and be updated with the newest information posted here.
Hello there! I just want to give you a huge thumbs up for your great info you have here on this post.
I am coming back to your blog for more soon.
I was curious if you ever thought of changing
the page layout of your website? Its very well
written; I love what youve got to say. But maybe you could a little more in the way of content so people
could connect with it better. Youve got an awful lot of
text for only having 1 or two images. Maybe you could space it out better?
When I initially left a comment I seem to have clicked on the -Notify me
when new comments are added- checkbox and now each time a comment is added I get 4 emails with the same comment.
Is there an easy method you are able to remove me from that service?
Kudos!
It’s amazing to pay a visit this site and reading the views of all colleagues on the topic of this piece of writing, while I am also
eager of getting know-how.
This text is priceless. When can I find out more?
Everything is very open with a precise clarification of
the challenges. It was truly informative. Your website
is extremely helpful. Many thanks for sharing!
WOW just what I was searching for. Came here by searching for buy soma online
Hello my family member! I wish to say that this post is amazing,
nice written and include approximately all vital infos.
I would like to look extra posts like this .
I do not even understand how I stopped up right here, however
I thought this publish was good. I do not know who you might be however definitely you’re going to a well-known blogger should
you are not already. Cheers!
I know this web site presents quality dependent articles or reviews
and additional material, is there any other web page which presents these
kinds of things in quality?
I savor, cause I found exactly what I used to be looking for.
You have ended my 4 day lengthy hunt! God Bless you man. Have a great day.
Bye
It’s going to be ending of mine day, except before finish I am reading
this impressive paragraph to improve my know-how.
Asking questions are truly good thing if you are not understanding anything completely,
but this article presents fastidious understanding even.
I have been surfing online more than three hours today, yet I never found any interesting
article like yours. It’s pretty worth enough for me.
Personally, if all site owners and bloggers made good content as you
did, the net will be much more useful than ever before.
I am genuinely delighted to read this web site posts which carries lots of useful facts,
thanks for providing these data.
It is perfect time to make some plans for the future and it’s time
to be happy. I’ve read this post and if I could I wish
to suggest you some interesting things or advice. Perhaps
you can write next articles referring to this article.
I desire to read more things about it!
Hey I know this is off topic but I was wondering if you knew of any widgets I
could add to my blog that automatically tweet my newest twitter updates.
I’ve been looking for a plug-in like this for quite some time
and was hoping maybe you would have some experience with something like this.
Please let me know if you run into anything.
I truly enjoy reading your blog and I look forward to your new
updates.
I am in fact glad to glance at this weblog posts which contains
plenty of useful data, thanks for providing such data.
Woah! I’m really digging the template/theme of this blog.
It’s simple, yet effective. A lot of times it’s difficult to get that “perfect balance” between superb usability and appearance.
I must say that you’ve done a superb job with this.
Also, the blog loads very fast for me on Safari. Exceptional Blog!
When someone writes an paragraph he/she maintains the thought of a user in his/her
mind that how a user can be aware of it. So that’s why
this article is perfect. Thanks!
It’s awesome to visit this website and reading the
views of all friends concerning this paragraph, while I am also keen of getting
familiarity.
Hi there every one, here every one is sharing such familiarity, thus it’s fastidious to read this weblog,
and I used to pay a quick visit this weblog everyday.
Wow! In the end I got a website from where I be able to really get useful facts regarding my study
and knowledge.
hi!,I really like your writing so so much! proportion we communicate more about your post on AOL?
I need an expert on this area to unravel my problem.
Maybe that’s you! Having a look ahead to look you.
Hello to every one, itโs really a good for me to visit this website, it
consists of useful Information.
Visit my new website in here “Click Here”
It’s difficult to find well-informed people on this subject, but
you sound like you know what you’re talking about!
Thanks
I’m not sure why but this web site is loading very slow for me.
Is anyone else having this problem or is it a
issue on my end? I’ll check back later on and see if the problem still exists.
Paragraph writing is also a excitement, if you know afterward you can write or
else it is complex to write.
[url=https://flagyl.quest/]flagyl metronidazole[/url]
[url=https://ivermectinforhumans.monster/]ivermectin 1 cream generic[/url]
[url=https://finpecia.quest/]finpecia 1 mg[/url]
[url=http://furosemidelasix.online/]lasix uk[/url]
[url=http://antabuse.monster/]disulfiram tablets online[/url] [url=http://cialisttabs.online/]generic cialis online pharmacy[/url] [url=http://acyclovir.monster/]can you buy acyclovir without a prescription[/url] [url=http://ivermectinttab.com/]stromectol cost[/url] [url=http://viagraonlineorder.com/]viagra without a doctor[/url]
[url=http://costofviagra.quest/]generic viagra best price[/url]
[url=https://tadalafiltabsonline.com/]buy tadalafil online usa[/url]
[url=http://cialiscost.online/]buy generic cialis online 40mg[/url]
[url=http://ventolin.online/]ventolin uk[/url]
[url=http://cialisttabs.online/]cialis pills 20mg[/url]
[url=http://aurogra.quest/]aurogra 100 for sale[/url] [url=http://paxil.online/]paxil canada pharmacy[/url] [url=http://generictadalafil.quest/]buy tadalafil tablets[/url] [url=http://escitalopram.quest/]lexapro 5 mg tablet[/url] [url=http://ivermectinttab.com/]stromectol otc[/url] [url=http://cialiscost.online/]where can i buy cialis online usa[/url] [url=http://cialisttabs.online/]buy cialis rx[/url] [url=http://finasteride.quest/]cheap finasteride[/url] [url=http://cialis10.online/]cialis 20 mg online pharmacy[/url] [url=http://viagraonlineorder.com/]cheap generic viagra fast delivery[/url]
[url=https://buycialispills.quest/]buy cialis 40 mg[/url]
[url=http://buyingviagra.quest/]female viagra pills uk[/url]
[url=http://cialis10.online/]cialis discount pharmacy[/url] [url=http://ivermectinatab.com/]ivermectin 5[/url] [url=http://kamagra.monster/]kamagra gel oral 50[/url] [url=http://zithromaxazithromycin.online/]azithromycin medicine[/url] [url=http://tadalafil20.online/]tadalafil price[/url] [url=http://atarax.online/]atarax 50 mg cost[/url] [url=http://ventolin.online/]ventolin discount[/url] [url=http://sildenafilgeneric.online/]sildenafil 100 mg tablets coupon[/url] [url=http://amoxil.quest/]amoxil 100mg[/url] [url=http://propeciafinasteride.online/]can i buy propecia over the counter in canada[/url]
[url=http://finpecia.quest/]finpecia online[/url] [url=http://albuterolventolin.online/]ventolin 4mg tab[/url] [url=http://canadianviagracheap.online/]can you order viagra from canada[/url] [url=http://iverpill.online/]stromectol where to buy[/url] [url=http://hydroxychloroquinepills.com/]plaquenil cheapest[/url]
[url=http://budesonide.online/]cost of budesonide capsules[/url] [url=http://cialis5mg.quest/]buy cialis no prescription[/url] [url=http://tadalafil20.online/]buy tadalafil online[/url] [url=http://ivermectinttab.com/]stromectol brand[/url] [url=http://viagraonlineorder.com/]viagra for sale in australia[/url] [url=http://sildenafilcitrate100.online/]sildenafil uk[/url] [url=http://genericsildenafilcitrate.quest/]sildenafil price comparison uk[/url] [url=http://cheapestviagra.online/]canadian viagra 100mg[/url] [url=http://cialis20mg.quest/]best cialis coupon[/url] [url=http://tadalafilatabs.online/]buy tadalafil online no prescription[/url]
[url=http://disulfiram.quest/]buy antabuse on line[/url]
[url=http://canadianviagracheap.online/]over the counter viagra usa[/url]
[url=https://ivermectinatab.com/]ivermectin cost canada[/url]
[url=https://cialisfromcanada.online/]cialis one a day[/url]
[url=http://sildenafilcitrate100.online/]cheap sildenafil 20 mg[/url]
[url=https://tadalafilktabs.online/]generic cialis tadalafil uk[/url]
[url=https://wellbutrin.monster/]buy wellbutrin[/url]
[url=http://stromectol.quest/]stromectol generic name[/url]
[url=https://cialiswithoutprescription.online/]cialis daily online[/url]
[url=http://wheretobuyviagra.quest/]generic viagra fast delivery[/url]
[url=https://sildenafilgeneric.online/]sildenafil 20 mg online rx[/url]
[url=https://bupropionwellbutrin.online/]bupropion 750 mg[/url]
[url=http://fluoxetine.quest/]fluoxetine 10mg[/url]
[url=http://canadiancialis.online/]can i buy cialis over the counter in usa[/url]
[url=https://ivermectinotc.quest/]ivermectin ireland[/url]
[url=https://kamagra.quest/]how much is kamagra[/url]
[url=http://propeciafinasteride.online/]5mg propecia tablets[/url]
[url=https://canadaviagra.quest/]cheap viagra 100[/url]
[url=http://lasixfurosemide.com/]where to buy furosemide[/url]
[url=https://amoxil.quest/]amoxil buy[/url]
[url=https://canadianpharmacyviagra.quest/]male viagra[/url]
Excellent goods from you, man. I’ve understand your stuff previous to and you are just extremely wonderful.
I really like what you’ve acquired here, really like what you’re
stating and the way in which you say it.
You make it entertaining and you still take care of to keep it sensible.
I cant wait to read much more from you. This is really
a wonderful web site.
[url=http://cheapsildenafil.online/]can i buy sildenafil in canada[/url]
Do you have a spam issue on this website; I also am
a blogger, and I was wanting to know your situation; we have
developed some nice practices and we are looking to trade solutions with others, please shoot me an e-mail if interested.
Informative article, totally what I wanted to find.
[url=http://trazodone.quest/]trazodone 100 mg coupon[/url] [url=http://gabapentinneurontin.online/]600 mg gabapentin tablet[/url] [url=http://furosemidelasix.online/]lasix tablets price[/url] [url=http://acyclovir.monster/]buy acyclovir online australia[/url] [url=http://ivermectinytabs.com/]where can i buy stromectol[/url] [url=http://pharmacyviagra.online/]cost of generic viagra[/url] [url=http://propeciafinasteride.online/]buy propecia cheap online[/url] [url=http://flagyl.quest/]buy flagyl online without prescription[/url] [url=http://ivermectinatab.com/]ivermectin buy online[/url] [url=http://canadaviagra.quest/]viagra from mexico to us[/url]
Amazing issues here. I’m very glad to look your article.
Thank you a lot and I’m taking a look ahead to contact you.
Will you please drop me a mail?
Thank you for another excellent article. The place else could anyone get that type of information in such a perfect approach of writing?
I have a presentation next week, and I’m at the search for such
info.
I’ve been exploring for a little for any high quality
articles or weblog posts on this kind of house .
Exploring in Yahoo I at last stumbled upon this web site. Reading this information So
i’m satisfied to convey that I’ve a very excellent uncanny
feeling I found out just what I needed. I so much undoubtedly will make certain to do not fail to remember this site and
give it a glance regularly.
What’s up to every one, as I am really keen of reading this web site’s post to be updated regularly.
It includes nice material.
I loved as much as you will receive carried out right here.
The sketch is attractive, your authored material stylish.
nonetheless, you command get bought an edginess
over that you wish be delivering the following.
unwell unquestionably come more formerly again since exactly
the same nearly a lot often inside case you shield this increase.
Hmm it appears like your website ate my first comment (it was extremely long) so I
guess I’ll just sum it up what I had written and say, I’m thoroughly
enjoying your blog. I too am an aspiring blog writer but I’m still new to
the whole thing. Do you have any points for beginner blog writers?
I’d certainly appreciate it.
[url=https://kamagra.monster/]kamagra oral jelly qatar[/url]
There is definately a great deal to find out about this topic.
I like all of the points you’ve made.
Hey I know this is off topic but I was wondering if you knew of any widgets I could
add to my blog that automatically tweet my newest twitter updates.
I’ve been looking for a plug-in like this
for quite some time and was hoping maybe you would have some experience with something like this.
Please let me know if you run into anything.
I truly enjoy reading your blog and I look forward to your new updates.
Very great post. I just stumbled upon your weblog and wanted to say that I have really enjoyed browsing your weblog posts.
After all I’ll be subscribing in your rss feed and I am hoping you write again very soon!
Thanks for sharing your thoughts on https://mwov8th4d.blogspot.com/. Regards
Hi, I do think this is an excellent site.
I stumbledupon it ๐ I’m going to revisit once again since i have
book marked it. Money and freedom is the greatest
way to change, may you be rich and continue to guide others.
Having read this I believed it was extremely enlightening.
I appreciate you taking the time and effort to put this informative article
together. I once again find myself spending
a lot of time both reading and posting comments. But
so what, it was still worthwhile!
What’s Happening i am new to this, I stumbled upon this I’ve found It positively useful and
it has helped me out loads. I’m hoping to contribute
& assist other users like its helped me. Great job.
Way cool! Some extremely valid points! I appreciate you writing
this write-up plus the rest of the site is also very good.
My developer is trying to convince me to move to .net from PHP.
I have always disliked the idea because of the costs.
But he’s tryiong none the less. I’ve been using WordPress on a variety of websites for about a year and am worried about switching
to another platform. I have heard great things about blogengine.net.
Is there a way I can transfer all my wordpress content into it?
Any kind of help would be really appreciated!
Generally I do not learn article on blogs, however I would like to say
that this write-up very forced me to take a look at and do it!
Your writing style has been amazed me. Thanks, very great post.
I know this if off topic but I’m looking into starting my own weblog and was curious what all
is needed to get set up? I’m assuming having
a blog like yours would cost a pretty penny? I’m not very internet smart so I’m not 100% certain. Any recommendations or advice would be greatly appreciated.
Thanks
I constantly spent my half an hour to read this webpage’s content daily along with a
cup of coffee.
Outstanding post however , I was wanting to know if you
could write a litte more on this subject? I’d be very thankful if you could elaborate a little bit more.
Kudos!
Greetings from Idaho! I’m bored at work so I decided to
browse your website on my iphone during lunch break.
I really like the information you provide here
and can’t wait to take a look when I get home. I’m surprised
at how fast your blog loaded on my phone .. I’m not
even using WIFI, just 3G .. Anyways, excellent blog!
Hi there, its nice post on the topic of media print, we all beaware of media is a wonderful source of information.
This site was… how do I say it? Relevant!! Finally
I have found something which helped me. Thanks!
I love it when people get together and share ideas.
Great site, stick with it!
[url=http://hydroxychloroquinepills.com/]plaquenil for ra[/url]
[url=http://canadaviagra.quest/]viagra online from india[/url] [url=http://canadianviagracheap.online/]discounted viagra[/url] [url=http://ivermectinytabs.com/]ivermectin canada[/url] [url=http://wellbutrin.monster/]75 mg bupropion[/url] [url=http://generictadalafil.quest/]tadalafil without prescription[/url] [url=http://albuterolventolin.online/]albuterol tablets[/url] [url=http://cialischeap.quest/]prescription cialis from canada[/url] [url=http://cymbalta.monster/]cymbalta 150 mg[/url] [url=http://lasixfurosemide.com/]furosemide 50 mg[/url] [url=http://cialisxrx.online/]cheap cialis 20mg australia[/url]
[url=http://amitriptyline.online/]amitriptyline 4[/url]
I do accept as true with all the ideas you have presented in your post.
They are really convincing and will certainly work.
Nonetheless, the posts are too short for novices.
May just you please extend them a little from subsequent time?
Thanks for the post.
Hi to every , as I am really eager of reading this blog’s post to
be updated on a regular basis. It includes fastidious data.
For latest information you have to pay a quick visit world
wide web and on internet I found this site as a most excellent website for most up-to-date updates.
Fantastic post.Really looking forward to read more.
I read this paragraph completely concerning the difference of newest and earlier technologies, it’s amazing
article.
[url=https://cialisxrx.online/]buy online cialis 5mg[/url]
You have made some good points there. I looked on the web for more info about the issue and found most individuals
will go along with your views on this web site.
[url=http://amoxil.quest/]amoxil pill[/url]
Thanks a lot for sharing this with all folks you really know what you are talking about!
Bookmarked. Please also consult with my site =). We can have
a link change contract between us
Appreciate this post. Let me try it out.
There is definately a lot to find out about this issue.
I love all the points you’ve made.
[url=https://cymbalta.today/]cymbalta discount[/url]
[url=http://ivermectinztab.online/]ivermectin rx[/url]
Very quickly this website will be famous amid all blogging and site-building users, due to it’s nice posts
Hi there, I found your web site by the use of Google at the
same time as looking for a related topic, your site got here up, it looks good.
I’ve bookmarked it in my google bookmarks.
Hi there, simply was aware of your blog via Google, and found
that it is truly informative. I am gonna watch out for brussels.
I’ll be grateful should you continue this in future. A lot of other people
will likely be benefited from your writing.
Cheers!
Thank you for the good writeup. It in fact was a amusement account it.
Look advanced to far added agreeable from you! However, how could we communicate?
[url=http://lexapro.live/]order generic lexapro online[/url] [url=http://furosemide.quest/]furosemide 40 mg cost[/url] [url=http://antabuse.today/]antabuse substitute[/url] [url=http://paxil.monster/]can you buy paxil over the counter[/url] [url=http://sildenafilnrx.com/]india sildenafil[/url] [url=http://100mgviagra.quest/]viagra pills uk[/url] [url=http://ivermecfin.online/]ivermectin buy online[/url] [url=http://viagra100mgpills.quest/]viagra over the counter us[/url] [url=http://genericcialispills.quest/]buy cialis europe[/url] [url=http://ivermectinpills.monster/]ivermectin 9mg[/url]
I think that everything published made a bunch of sense.
But, think about this, what if you were to write a awesome post title?
I am not suggesting your information is not good., but what if
you added a post title to maybe get a person’s attention? I mean Types of Beams in Engineering Mechanics – Structures Explained is a
little vanilla. You could look at Yahoo’s home page and
note how they create post headlines to get people interested.
You might try adding a video or a pic or two to grab readers interested about what
you’ve got to say. In my opinion, it might bring your website a little livelier.
Hi outstanding website! Does running a blog like this take a great deal of work?
I have absolutely no knowledge of programming however I was
hoping to start my own blog soon. Anyhow, should you have any ideas
or techniques for new blog owners please share. I understand this is off subject
nevertheless I just wanted to ask. Cheers!
[url=https://atarax.live/]atarax discount[/url]
[url=https://cialismtablets.com/]cialis tablets 5mg price[/url]
It’s remarkable designed for me to have a site, which is good in favor of my experience.
thanks admin
It’s very easy to find out any topic on net as compared to books,
as I found this article at this web site.
Thanks for the auspicious writeup. It actually was
once a leisure account it. Look complicated to more delivered agreeable from you!
By the way, how can we keep in touch?
[url=http://synthroid.today/]synthroid online without prescription[/url]
Greetings from Los angeles! I’m bored to tears at work so I decided to browse your website on my iphone during lunch
break. I really like the knowledge you present here and can’t wait to take a
look when I get home. I’m surprised at how quick your blog loaded on my phone ..
I’m not even using WIFI, just 3G .. Anyways, fantastic blog!
Greetings! This is my 1st comment here so I just wanted to give a
quick shout out and say I really enjoy reading your articles.
Can you suggest any other blogs/websites/forums that cover
the same subjects? Thanks for your time!
[url=https://ivermectinetabs.com/]ivermectin oral[/url]
[url=https://sildenafilcitrategn.com/]sildenafil cost in india[/url]
This is my first time pay a quick visit at here and i am genuinely
impressed to read everthing at alone place.
Hey There. I found your blog using msn. This is an extremely well written article.
I will be sure to bookmark it and return to read more
of your useful information. Thanks for the post.
I’ll definitely return.
Hi there to every body, it’s my first visit of this blog; this webpage carries awesome and actually good data in favor of readers.
Very descriptive blog, I loved that bit. Will there be a part
2?
Post writing is also a excitement, if you be acquainted with after that you can write otherwise it is complex to write.
[url=http://anafranil.today/]anafranil capsules[/url]
These are really fantastic ideas in on the topic of blogging.
You have touched some nice factors here. Any
way keep up wrinting.
Thanks , I have just been looking for information approximately this topic for a
while and yours is the greatest I have came
upon till now. But, what in regards to the conclusion?
Are you certain concerning the source?
[url=https://viagra100mgprice.quest/]viagra 100mg tablet buy online[/url]
Hey! I know this is sort of off-topic but I needed to ask.
Does running a well-established blog such as yours require a large amount of work?
I’m brand new to running a blog but I do write in my journal on a daily
basis. I’d like to start a blog so I can share my own experience and views online.
Please let me know if you have any suggestions or tips for new aspiring blog owners.
Appreciate it!
Hey! Do you know if they make any plugins to protect against hackers?
I’m kinda paranoid about losing everything
I’ve worked hard on. Any suggestions?
I’m extremely impressed with your writing skills
and also with the layout on your blog. Is this a paid theme or
did you customize it yourself? Either way keep up the
nice quality writing, it’s rare to see a nice blog like this one today.
[url=https://anafranil.quest/]anafranil for anxiety[/url]
[url=http://100mgviagra.quest/]viagra brand price[/url]
[url=https://ivermectintablets.monster/]ivermectin 20 mg[/url]
[url=http://zoloft.live/]average cost of zoloft prescription[/url] [url=http://buytadalafilwhere.com/]tadalafil 5 mg for sale without prescription[/url] [url=http://atarax.live/]atarax 25[/url] [url=http://cialiszr.com/]buy cialis tablets australia[/url] [url=http://cialiswise.com/]buy cialis online from india[/url]
It’s difficult to find experienced people about this topic, but you seem
like you know what you’re talking about! Thanks
What’s up everybody, here every one is sharing these kinds of
familiarity, therefore it’s good to read this blog, and I used to go to see this web site daily.
What’s up, I check your new stuff daily. Your writing style is awesome, keep up
the good work!
Howdy, i read your blog from time to time and i own a similar
one and i was just curious if you get a lot of spam
responses? If so how do you stop it, any plugin or anything you can advise?
I get so much lately it’s driving me mad so any help
is very much appreciated.
Hi mates, fastidious post and fastidious urging commented here, I am actually enjoying by these.
That is a great tip particularly to those fresh to the blogosphere.
Short but very accurate infoโฆ Appreciate your sharing this one.
A must read article!
excellent put up, very informative. I wonder why the opposite experts of this sector don’t realize this.
You should continue your writing. I’m confident, you’ve a huge readers’ base already!
I’m impressed, I have to admit. Rarely do I come across a blog that’s
both educative and entertaining, and let me tell you,
you have hit the nail on the head. The problem is something which too few men and women are speaking
intelligently about. I am very happy that I came across this in my hunt for something
relating to this.
[url=https://tadalafillily.com/]tadalafil citrate[/url]
Very energetic blog, I enjoyed that a lot.
Will there be a part 2?
[url=http://cialisgk.com/]order cialis online cheap[/url]
Hello! I know this is kinda off topic nevertheless I’d figured I’d ask.
Would you be interested in trading links or maybe
guest authoring a blog article or vice-versa? My blog covers a lot of the same subjects as yours
and I think we could greatly benefit from each other. If you happen to be
interested feel free to send me an e-mail. I look forward to hearing from you!
Wonderful blog by the way!
[url=https://finasterideforsale.monster/]finasteride where can i buy[/url]
What’s up mates, pleasant piece of writing and
nice arguments commented here, I am truly enjoying by these.
[url=http://genericcialispills.quest/]discount generic cialis[/url]
I visit each day a few blogs and information sites to read
content, except this webpage gives quality based content.
Hi there to every one, the contents present at this website are actually amazing for people experience, well, keep up the good work fellows.
Does your website have a contact page? I’m having problems locating it but, I’d
like to shoot you an email. I’ve got some ideas for your blog you might be interested in hearing.
Either way, great blog and I look forward to seeing it expand over time.
Wonderful, what a weblog it is! This blog gives valuable data to us,
keep it up.
This article will help the internet users for setting up
new weblog or even a weblog from start to end.
Hi, I desire to subscribe for this blog to take most recent updates, so where can i do it please help.
Your means of telling the whole thing in this post is actually pleasant, every one be capable
of without difficulty be aware of it, Thanks a lot.
Wow, wonderful blog layout! How long have you been blogging for?
you make blogging look easy. The overall look of your website is
fantastic, let alone the content!
Today, I went to the beachfront with my children. I found a sea
shell and gave it to my 4 year old daughter and
said “You can hear the ocean if you put this to your ear.” She
put the shell to her ear and screamed. There was a hermit crab inside and
it pinched her ear. She never wants to go back!
LoL I know this is entirely off topic but I had to tell
someone!
Hello i am kavin, its my first occasion to commenting anywhere, when i
read this piece of writing i thought i could also create comment due to this good paragraph.
[url=http://wellbutrin.live/]wellbutrin drug[/url]
Thanks for finally talking about > Types of Beams in Engineering Mechanics
– Structures Explained < Loved it!
Greetings! Very helpful advice in this particular post!
It’s the little changes that will make the most important changes.
Thanks a lot for sharing!
Good post. I learn something new and challenging on sites I stumbleupon everyday.
It’s always interesting to read content from other authors and use a little
something from their sites.
Greate pieces. Keep posting such kind of information on your
page. Im really impressed by your blog.
Hello there, You’ve done an incredible job. I’ll certainly digg it and individually suggest to my
friends. I am sure they’ll be benefited from this website.
Thanks a bunch for sharing this with all of us you actually know what
you are talking about! Bookmarked. Please also seek advice
from my site =). We will have a hyperlink exchange contract among us
Hello, its good post regarding media print, we all be
aware of media is a great source of facts.
[url=http://cialisgk.com/]cialis daily without prescription[/url]
[url=http://furosemide.quest/]furosemide 40 mg tablets online[/url]
I am curious to find out what blog platform you have been working
with? I’m experiencing some minor security problems with my latest website and I
would like to find something more risk-free. Do you have any solutions?
Admiring the hard work you put into your website and in depth information you provide.
It’s awesome to come across a blog every once in a while
that isn’t the same out of date rehashed information. Great
read! I’ve saved your site and I’m adding your RSS feeds to
my Google account.
[url=http://viagraxo.com/]viagra india cheap[/url]
Way cool! Some extremely valid points! I appreciate you writing this post plus the rest
of the site is also really good.
[url=https://paxil.monster/]paxil 300 mg[/url]
I used to be recommended this blog through my cousin. I’m not sure whether or not this
submit is written via him as nobody else recognize such distinctive approximately my problem.
You are amazing! Thank you!
I was wondering if you ever thought of changing the layout of your
website? Its very well written; I love what youve got to say.
But maybe you could a little more in the way of content
so people could connect with it better. Youve got an awful lot of text for only having 1 or
two pictures. Maybe you could space it out better?
It’s actually a great and helpful piece of information. I’m satisfied that you simply shared this useful info with
us. Please stay us informed like this. Thank you for sharing.
[url=http://cialiswithnoprescription.com/]where to order cialis[/url]
[url=http://sildenafilcitrategn.com/]sildenafil 100mg price canada[/url]
If some one wants to be updated with most up-to-date technologies then he must be pay a visit this
web page and be up to date daily.
[url=https://malegrapills.quest/]malegra 50[/url]
hi!,I really like your writing so much! proportion we keep in touch more approximately your post on AOL?
I need a specialist on this house to unravel my problem.
May be that’s you! Looking ahead to look you.
Good article! We will be linking to this great content on our
site. Keep up the great writing.
[url=http://cialiszr.com/]cialis soft tabs generic[/url]
[url=http://cialisseven.com/]can you order cialis online[/url] [url=http://buyivermectinpills.quest/]ivermectin purchase[/url] [url=http://trazodone.live/]trazodone 50 mg price[/url] [url=http://lexapro.live/]lexapro 20[/url] [url=http://trazodonepills.live/]trazodone 100mg brand name[/url]
whoah this weblog is wonderful i like studying your posts.
Keep up the good work! You recognize, a lot of persons are searching around for this info, you can aid them greatly.
Very descriptive blog, I enjoyed that bit. Will there be
a part 2?
This site was… how do I say it? Relevant!!
Finally I have found something which helped me. Many thanks!
Ahaa, its pleasant dialogue about this piece of writing here at this webpage, I have read all that,
so now me also commenting here.
Hi there I am so happy I found your webpage, I really found you by mistake, while
I was looking on Bing for something else, Anyways I am here now and would just like to say thank you for
a tremendous post and a all round exciting blog (I also love the theme/design), I
donโt have time to read it all at the minute but I have saved
it and also added your RSS feeds, so when I have time
I will be back to read a lot more, Please do keep up
the fantastic jo.
Thanks in favor of sharing such a nice thinking, piece of writing is nice, thats why
i have read it completely
continuously i used to read smaller articles which also clear their motive,
and that is also happening with this article which I am reading here.
[url=https://synthroid.today/]synthroid 200 mg[/url]
Hello, i think that i saw you visited my site thus
i came to โreturn the favorโ.I am attempting to find things to improve my web site!I suppose its ok to use a
few of your ideas!!
Hi there just wanted to give you a quick heads up.
The words in your content seem to be running off the screen in Safari.
I’m not sure if this is a format issue or something to do with internet browser compatibility but I figured
I’d post to let you know. The design and style look great though!
Hope you get the issue resolved soon. Many thanks
[url=https://paxiltabs.world/]paroxetine pill costs[/url]
Hi there! I just want to offer you a huge thumbs up for
the great info you’ve got right here on this post.
I am returning to your site for more soon.
Every weekend i used to pay a visit this site, because i want enjoyment, for the reason that this this site
conations truly pleasant funny data too.
Thank you for the auspicious writeup. It in fact was a amusement account it.
Look advanced to far added agreeable from you! By the way, how
could we communicate?
It is really a great and helpful piece of information. I am happy that
you shared this helpful info with us. Please stay us informed like this.
Thank you for sharing.
Hurrah! At last I got a web site from where I be capable
of in fact get useful information regarding my study and knowledge.
I have been exploring for a little bit for any high quality articles
or weblog posts in this sort of space . Exploring in Yahoo I ultimately
stumbled upon this web site. Reading this information So
i am glad to express that I’ve an incredibly just right uncanny
feeling I found out just what I needed. I such a lot
no doubt will make sure to don?t forget this web
site and provides it a look regularly.
I’m not sure where you’re getting your info, but great topic.
I needs to spend some time learning more or understanding more.
Thanks for excellent info I was looking for this information for my mission.
[url=http://azithromycinpills.monster/]azithromycin 250mg coupon[/url]
[url=https://anafranil.quest/]anafranil capsules[/url]
You actually make it seem so easy with your presentation but I find this topic to be actually something which I think I would never understand.
It seems too complex and extremely broad for
me. I’m looking forward for your next post, I will try
to get the hang of it!
Have you ever thought about creating an e-book or guest authoring on other sites?
I have a blog based on the same ideas you discuss and
would really like to have you share some stories/information. I know my visitors would value your work.
If you’re even remotely interested, feel free to send me an e-mail.
Heya i’m for the primary time here. I came across this board and I find It truly useful & it helped me out a lot.
I hope to offer one thing again and help others like you
aided me.
My brother recommended I might like this website.
He was entirely right. This post actually made my
day. You can not imagine just how much time I had spent for this information! Thanks!
[url=http://malegra.live/]malegra 100[/url]
[url=https://viagraefi.com/]viagra tablet canada[/url]
My programmer is trying to persuade me to
move to .net from PHP. I have always disliked the idea because of the
costs. But he’s tryiong none the less. I’ve been using
WordPress on several websites for about a year and am concerned about switching to another platform.
I have heard great things about blogengine.net. Is there a way I can transfer all
my wordpress posts into it? Any help would be greatly appreciated!
This design is incredible! You definitely know how to keep a
reader entertained. Between your wit and your videos, I
was almost moved to start my own blog (well, almost…HaHa!) Great job.
I really enjoyed what you had to say, and more than that, how you
presented it. Too cool!
What’s up, its good piece of writing concerning media print, we all
be aware of media is a great source of information.
Heya i am for the first time here. I found this board and I
find It really useful & it helped me out much. I hope to give
something back and aid others like you helped me.
Everything is very open with a really clear clarification of
the challenges. It was really informative. Your site is useful.
Thank you for sharing!
When I initially left a comment I seem to have clicked on the -Notify me
when new comments are added- checkbox and from now
on each time a comment is added I recieve 4 emails with the exact
same comment. Perhaps there is an easy method you can remove me from that service?
Appreciate it!
What’s up to all, it’s genuinely a nice for me to
pay a quick visit this site, it contains valuable Information.
Awesome things here. I am very satisfied to peer
your article. Thanks a lot and I am having a look ahead to touch you.
Will you kindly drop me a mail?
[url=https://cialismtablets.com/]cialis buy india[/url]
Hello I am so thrilled I found your weblog,
I really found you by error, while I was researching on Bing for something else,
Nonetheless I am here now and would just like to say many thanks for
a remarkable post and a all round thrilling blog (I also
love the theme/design), I don’t have time to look over it all at the moment but I have bookmarked it and also
included your RSS feeds, so when I have time I will
be back to read more, Please do keep up the fantastic work.
My brother suggested I might like this web site. He
was totally right. This post actually made my day.
You can not imagine just how much time I
had spent for this information! Thanks!
[url=http://budesonide.monster/]budesonide 0.25[/url]
Everyone loves it when people come together and share thoughts.
Great site, stick with it!
This post provides clear idea in favor of the new
viewers of blogging, that actually how to do running a blog.
[url=http://cymbalta.quest/]cymbalta 40 mg[/url] [url=http://atarax.live/]generic atarax[/url] [url=http://cialisict.com/]cialis in canada cost[/url] [url=http://buyviagraonlinepharmacy.com/]uk viagra buy[/url] [url=http://medviagra.com/]drugstore viagra[/url] [url=http://ivermectinztab.online/]ivermectin 1 cream generic[/url] [url=http://ivermectinntabs.com/]ivermectin 15 mg[/url] [url=http://sildenafilpillcost.com/]sildenafil price in india[/url] [url=http://tadalafilonlinesale.com/]tadalafil 5mg daily[/url] [url=http://cialis20.quest/]cialis us pharmacy[/url]
I loved as much as you will receive carried
out right here. The sketch is attractive, your authored subject matter
stylish. nonetheless, you command get bought an impatience over that you wish be
delivering the following. unwell unquestionably come more formerly again as exactly the same
nearly very often inside case you shield this hike.
Spot on with this write-up, I actually believe this amazing
site needs a lot more attention. I’ll probably be returning to read through more,
thanks for the advice!
Woah! I’m really enjoying the template/theme of this site.
It’s simple, yet effective. A lot of times it’s tough
to get that “perfect balance” between usability and appearance.
I must say that you’ve done a great job with this.
In addition, the blog loads super quick for me on Safari.
Superb Blog!
Thank you for the auspicious writeup. It in fact
was a amusement account it. Look advanced to far added agreeable from you!
By the way, how could we communicate?
This design is wicked! You obviously know how to keep a reader amused.
Between your wit and your videos, I was almost moved to start my own blog (well, almost…HaHa!) Fantastic
job. I really loved what you had to say, and more than that, how you presented it.
Too cool!
Right here is the right website for anybody who wishes to
understand this topic. You realize so much its almost tough to argue with you (not that I really will
need toโฆHaHa). You definitely put a new spin on a topic that has been written about for many years.
Excellent stuff, just excellent!
[url=http://viagra100mgprice.quest/]price of viagra 100mg[/url] [url=http://strattera.quest/]strattera generic costs[/url] [url=http://fluoxetine.live/]where can i buy fluoxetine online[/url] [url=http://tadalafilbrem.com/]tadalafil buy[/url] [url=http://ivermectinztabs.com/]buy ivermectin[/url] [url=http://tadalafilonlinesale.com/]tadalafil 100mg best price[/url] [url=http://aurogra.online/]aurogra 100[/url] [url=http://ivermectinltab.com/]ivermectin buy canada[/url] [url=http://viagrazpill.com/]where can i buy real viagra online[/url] [url=http://viagrammc.com/]generic viagra from india online[/url]
Hey there, You’ve done an incredible job. I’ll definitely digg it and personally
recommend to my friends. I’m confident they’ll be benefited from this
website.
I love it when people come together and share thoughts. Great website,
stick with it!
Wonderful blog! Do you have any helpful hints for aspiring writers?
I’m hoping to start my own website soon but I’m a little
lost on everything. Would you recommend starting with a free platform like WordPress or
go for a paid option? There are so many options out
there that I’m totally confused .. Any suggestions?
Thank you!
What’s up to every , because I am really keen of reading this blog’s post to be updated regularly.
It includes fastidious data.
[url=http://buytadalafilwhere.com/]tadalafil tablet online in india[/url]
Amazing blog! Is your theme custom made or did you download it
from somewhere? A design like yours with a few simple adjustements
would really make my blog jump out. Please let me know where you
got your theme. Bless you
Hey there! I could have sworn I’ve been to this website before but
after checking through some of the post I realized it’s new to me.
Anyways, I’m definitely glad I found it and I’ll be bookmarking
and checking back frequently!
I enjoy looking through a post that will make men and women think.
Also, thanks for permitting me to comment!
Normally I do not learn article on blogs, however I
wish to say that this write-up very forced me to try and
do so! Your writing taste has been surprised me.
Thank you, very nice article.
This is my first time pay a quick visit at here and i
am truly impressed to read everthing at one place.
Heya i am for the first time here. I came across this
board and I find It really useful & it helped me out
a lot. I hope to give something back and aid others like you helped
me.
Excellent blog here! Also your site loads up very fast!
What web host are you using? Can I get your affiliate link to
your host? I wish my site loaded up as fast as yours lol
It’s an awesome article in support of all the internet people; they will obtain benefit from it
I am sure.
I read this post completely concerning the difference of hottest and preceding technologies,
it’s awesome article.
If you would like to get a great deal from this paragraph then you have to apply
these techniques to your won weblog.
It’s amazing in favor of me to have a website, which is useful designed for my knowledge.
thanks admin
That is a very good tip particularly to those fresh to the blogosphere.
Short but very precise infoโฆ Thank you for sharing this one.
A must read post!
It’s actually very complex in this busy life to listen news on TV,
therefore I only use the web for that purpose, and take the newest information.
Fantastic blog! Do you have any recommendations for aspiring writers?
I’m planning to start my own site soon but I’m a little lost on everything.
Would you suggest starting with a free platform like WordPress or go for
a paid option? There are so many choices out there that I’m totally overwhelmed ..
Any ideas? Kudos!
[url=http://wellbutrin.live/]cheap wellbutrin xl[/url]
I am really impressed with your writing skills as well as with the layout
on your blog. Is this a paid theme or did you modify it yourself?
Anyway keep up the nice quality writing, it is rare to see a
nice blog like this one today.
Excellent post. I used to be checking continuously this blog and I’m inspired!
Extremely useful info particularly the last phase ๐ I
take care of such info a lot. I was looking for this particular information for a long time.
Thank you and good luck.
That is a really good tip especially to those new to the blogosphere.
Simple but very precise infoโฆ Many thanks for sharing this one.
A must read post!
Way cool! Some very valid points! I appreciate you writing this article and also the rest of the site is also
very good.
I couldn’t resist commenting. Well written!
[url=http://malegrapills.quest/]malegra 25 mg[/url]
Hi, just wanted to mention, I enjoyed this article.
It was practical. Keep on posting!
We stumbled over here coming from a different page
and thought I may as well check things out. I like what I see so now i’m following you.
Look forward to going over your web page repeatedly.
[url=https://ataraxpills.monster/]hydroxyzine atarax[/url]
Great goods from you, man. I have understand your stuff previous to and you’re
just extremely excellent. I actually like what you’ve acquired here, certainly
like what you’re stating and the way in which you say it.
You make it entertaining and you still take care
of to keep it wise. I can not wait to read much more from you.
This is actually a great site.
Your style is really unique in comparison to other folks I’ve
read stuff from. Many thanks for posting when you have the opportunity, Guess I will just book mark
this blog.
whoah this weblog is excellent i love studying your articles.
Stay up the good work! You recognize, lots of individuals